Hiện thực phát hiện đoạn thẳng dùng Hough Transform

  May 18, 2019      2m      0   

 

OpenCV - tut 13: Hiện thực phát hiện đoạn thẳng

Môi trường "hành sự"

• Linux (bài viết sử dụng Ubuntu 16.04)
• OpenCV (bài viết sử dụng OpenCV 3.4.1)
• Python (bài viết sử dụng Python 3.5.5)
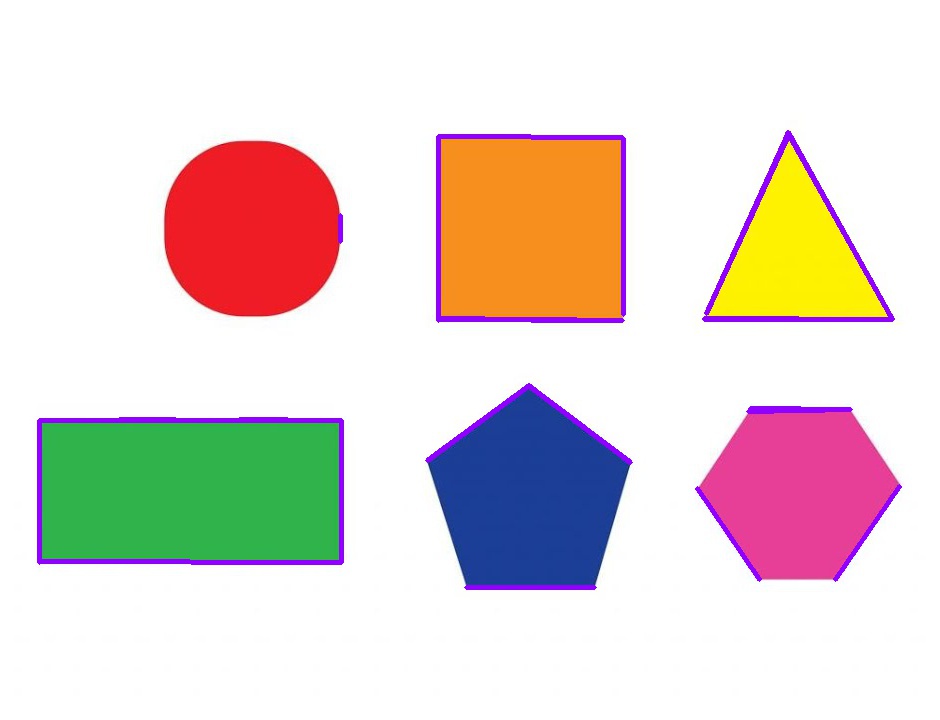
• Ảnh mẫu để xử lý: geometry.jpg

Bạn có thể download ảnh mẫu về:

geometry.jpg (Nguồn: Lụm trên mạng)

Hiện thực phát hiện đoạn thẳng dùng Hough Transform

Ở bài viết trước, mình đã hiện thực giải thuật Hough Transform cho phát hiện đường thẳng. Do đó, bài này là phiên bản mở rộng bằng cách phát hiện ra các đoạn thẳng trên đường thẳng đó. Như kết quả của bài trước, ta chỉ biết đường thẳng chạy xuyên suốt ảnh, mà không biết các đoạn thẳng nào là cạnh của đối tượng (hình chữ nhật, hình vuông, tam giác, …). Trong bài viết này, ta cần viết thêm một chút ở bước hậu xử lý để từ thông tin đường thẳng trên ta sẽ trích xuất ra đoạn thẳng bằng cách đối chiếu với thông tin đặc trưng cạnh (các pixel cạnh).

Ý tưởng hiện thực:

1. Thống kê các pixel cạnh nào thuộc đường thẳng nào (rho, theta) bằng cách duyệt từng pixel cạnh, tính giá trị rho và so sánh xem nó có khớp với đường thẳng đang xét. Nếu có ta lưu vào danh sách trong từ điển. Siêu tham số cho quá trình xử lý này là rho_delta (default=1).

line_px_dict = {}
for (rho, theta) in line_idx:
    line_px_dict[(rho, theta)] = [] # init empty list for the key (rho, theta)
    for row_idx in range(idx.shape[0]): # idx dim: 4468 x 2
        point_x, point_y = idx[row_idx,0], idx[row_idx,1]
        rho_point = point_x*np.cos(theta) + point_y*np.sin(theta) # ρ=xcosθ+ysinθ
        if abs(int(rho_point) - rho) <= rho_delta:
            line_px_dict[(rho, theta)].append((point_x, point_y))
        pass
    pass

1. Xem xét các pixel thuộc mỗi đường thẳng, từ đó kiểm tra xem pixel sau có liền kề pixel trước hay không (bằng cách so sánh delta x và delta y của chúng với một siêu tham số xác định trước là px_delta (default=5)). Nếu chúng liền kề thì ta lặp tiếp, nếu không thì đoạn danh sách các pixel vừa duyệt qua vừa tạo thành 1 đoạn thẳng –> kiểm tra "độ dài" (số pixel) của đoạn thẳng vừa rồi có vượt ngưỡng siêu tham số min_line_length_percent (default=0.15) so với tổng số pixel thuộc đường đang xét hay không. Nếu nhỏ hơn ngưỡng (tức đây có thể là nhiễu), bỏ qua đoạn thẳng đó. Nếu lớn hơn ngưỡng thì đây là đoạn thẳng cần tìm.

Code hiện thực đầy đủ cho hiện thực ý tưởng trên:

hough_shape.py

import math
import cv2
import numpy as np

# reference: https://docs.opencv.org/master/d6/d10/tutorial_py_houghlines.html
def my_hough(img, rho=1, theta=np.pi/180, threshold=100, rho_delta=1, px_delta=5, min_line_length_percent=0.15):
    img_height, img_width = img.shape[:2]
    diagonal_length = int(math.sqrt(img_height*img_height + img_width*img_width))
    
    print('[My Hough] Img Height: %d | Img Width: %d | Img Diagonal Length: %d' % (img_height, img_width, diagonal_length))
    
    num_rho = int(diagonal_length / rho)
    num_theta = int(np.pi / theta)
    
    edge_matrix = np.zeros([2*num_rho+1, num_theta]) # dim: num_rho x num_theta
    
    print('[My Hough] Edge Matrix Dim: %d x %d' % (edge_matrix.shape[0], edge_matrix.shape[1]))
    
    idx	= np.squeeze(cv2.findNonZero(img)) # dim: 4468 x 2 (example, number of rows = number of white pixel on image processed by canny edge algorithm!)
    
    range_theta = np.arange(0, np.pi, theta)   
    theta_matrix = np.stack((np.cos(np.copy(range_theta)), np.sin(np.copy(range_theta))), axis=-1) # dim: 180 x 2
    
    vote_matrix = np.dot(idx, np.transpose(theta_matrix)) # => (4468 x 2) * (180 x 2)T = (4468 x 2) * (2 x 180) = 4468 x 180
    print('[My Hough] Vote Matrix Dim: %d x %d' % (vote_matrix.shape[0], vote_matrix.shape[1]))
    
    # loop on vote matrix and accumulate values on edge matrix
    for vr in range(vote_matrix.shape[0]):
        for vc in range(vote_matrix.shape[1]):
            rho_pos = int(round(vote_matrix[vr, vc]))+num_rho
            edge_matrix[rho_pos, vc] += 1
    
    print('[My Hough] Sum of Edge Matrix = %d | Max = %d | Min = %d' % (int(np.sum(edge_matrix)), int(np.max(edge_matrix)), int(np.min(edge_matrix))))
    
    line_idx = np.where(edge_matrix > threshold)
    
    rho_values = list(line_idx[0])
    rho_values = [r-num_rho for r in rho_values]
    theta_values = list(line_idx[1])
    theta_values = [t/180.0*np.pi for t in theta_values]
    
    line_idx = list(zip(rho_values, theta_values))
    # line_idx: [(-626, 2.6354471705114375), (-625, 2.6354471705114375), (-304, 2.548180707911721), (-11, 2.2165681500327987), (39, 0.0), (136, 1.5707963267948966), (319, 1.5707963267948966), (320, 1.5707963267948966), (341, 0.0), (408, 1.5707963267948966), (419, 1.5707963267948966), (422, 1.5533430342749532), (438, 0.0), (562, 1.5707963267948966), (588, 1.5707963267948966), (623, 0.0), (624, 0.9250245035569946), (733, 0.2792526803190927), (772, 0.41887902047863906), (773, 0.41887902047863906), (1017, 0.593411945678072)]
    
    #line_idx = [[li] for li in line_idx]
    
    line_px_dict = {}
    # line_px_dict: {
    #    (rho_0, theta_0): [(x0,y0), (x1,y1), ...],
    #    ...
    #}
    for (rho, theta) in line_idx:
        line_px_dict[(rho, theta)] = [] # init empty list for the key (rho, theta)
        for row_idx in range(idx.shape[0]): # idx dim: 4468 x 2
            point_x, point_y = idx[row_idx,0], idx[row_idx,1]
            rho_point = point_x*np.cos(theta) + point_y*np.sin(theta) # ρ=xcosθ+ysinθ
            if abs(int(rho_point) - rho) <= rho_delta:
                line_px_dict[(rho, theta)].append((point_x, point_y))
            pass
        pass
    
    # find (xmin, ymin) and (xmax, ymax) of every (rho, theta) in line_px_dict
    line_result = []
    for (rho, theta) in line_px_dict.keys():
        point_list = line_px_dict[(rho, theta)] # [(x0,y0), (x1,y1), ...]
        point_list.sort(key=lambda tup: tup[0]) # sort by x
        
        pf_idx = 0
        pfrom = point_list[pf_idx]
        pcurrent = pfrom
        for p_idx in range(len(point_list)):
            pto = point_list[p_idx]
            if abs(pto[0]-pcurrent[0]) <= px_delta and abs(pto[1]-pcurrent[1]) <= px_delta and p_idx != len(point_list)-1:
                pcurrent = pto
            else:
                pt_idx = p_idx-1 if p_idx != len(point_list)-1 else p_idx
                pto = point_list[pt_idx]
                line_length_percent = (pt_idx-pf_idx)/len(point_list)
                
                if line_length_percent >= min_line_length_percent:
                    line_result.append([pfrom, pto])
                else:
                    pass
                pf_idx = p_idx
                pfrom = point_list[p_idx]
                pcurrent = pfrom

    return line_result

def main():
    # read image
    img = cv2.imread('geometry.jpg')
    # convert to gray scale
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # color -> gray
    edges = cv2.Canny(gray, 50, 150, apertureSize=3) # https://docs.opencv.org/2.4/modules/imgproc/doc/feature_detection.html?highlight=canny#canny
    cv2.imwrite('geo_canny.jpg', edges)
    
    # IMPLEMENT HOUGH ALGORITHM MYSELF!
    lines = my_hough(edges, rho=1, theta=np.pi/180, threshold=100)
    for line in lines:
        (x1, y1) = line[0]
        (x2, y2) = line[1]
        cv2.line(img, (x1,y1), (x2,y2),(255,0,143), 3)    
    cv2.imwrite('geo_shape.jpg',img)

if __name__ == "__main__":
    main()
    print('* Follow me @ ' + "\x1b[1;%dm" % (34) + ' https://www.facebook.com/minhng.info/' + "\x1b[0m")
    print('* Join GVGroup for discussion @ ' + "\x1b[1;%dm" % (34) + 'https://www.facebook.com/groups/ip.gvgroup/' + "\x1b[0m")
    print('* Thank you ^^~')    

Hình kết quả:

geo_shape.jpg

Nhận xét về giải thuật phát hiện đoạn thẳng:

• Dùng vòng lặp, khối lượng tính toán xử lý lớn nên tốc độ còn chậm.
• Cần hiểu rõ tính chất để điều chỉnh phù hợp các siêu tham số: rho_delta, px_delta, min_line_length_percent.
• Hiện thực giải thuật còn chậm nên chỉ có thể áp dụng vào các ảnh hình học đơn giản.

---

Cảm ơn bạn đã theo dõi bài viết. Hãy kết nối với tớ nhé!

• Minh: https://www.facebook.com/minhng.info
• Khám phá xử lý ảnh - GVGroup: https://www.facebook.com/groups/ip.gvgroup

Khám phá xử lý ảnh - GVGroup

Danh sách bài viết series OpenCV:

• Hashtag #OpenCV
• Tut 1: Xử lý ảnh - OpenCV đọc ghi hình ảnh (code Python và C++)
• Tut 1.1: Xử lý ảnh - Cấu trúc dữ liệu ảnh trong OpenCV. Pixel là gì?
• Tut 1.2: Xử lý ảnh - Chuyển đổi ảnh OpenCV sang Pillow và ngược lại
• Tut 2: Xử lý ảnh - OpenCV resize, crop và padding hình ảnh (code Python và C++)
• Tut 3: Xử lý ảnh - OpenCV biến đổi mức sáng hình ảnh (code Python)
• Tut 4: Xử lý ảnh - OpenCV vùng quan tâm (ROI) là gì? (code Python)
• Tut 4.1: Xử lý ảnh - OpenCV: vẽ văn bản, đường thẳng, mũi tên, hình chữ nhật, hình tròn, ellipse, đa giác
• Tut 4.2: Xử lý ảnh - Pha trộn ảnh trong OpenCV (blending)
• Tut 5: Xử lý ảnh - OpenCV ảnh nhị phân
• Tut 6: Xử lý ảnh - OpenCV cân bằng sáng (histogram equalization)
• Tut 7: Xử lý ảnh - OpenCV kỹ thuật cửa sổ trượt (sliding window)
• Tut 8: Xử lý ảnh - Convolution là gì?
• Tut 9: Xử lý ảnh - Làm mờ ảnh (blur)
• Tut 10: Xử lý ảnh - Gradient của ảnh là gì?
• Tut 11: Xử lý ảnh - Phát hiện cạnh Canny (Canny Edge Detection)
• Tut 12: Xử lý ảnh - Phát hiện đường thẳng bằng Hough Transform (Hough Line)
• Tut 13: Xử lý ảnh - Hiện thực phát hiện đoạn thẳng dùng Hough Transform (Hough Line)
• Tut 14: Xử lý ảnh - Giải thuật phân vùng Region Growing trên ảnh màu
• Tut 15: Xử lý ảnh - Giải thuật Background Subtraction trên ảnh màu
• Tut 16: Xử lý ảnh - Frame Subtraction để phát hiện chuyển động trong video
• Tut 17: Xử lý ảnh - HOG - Histograms of Oriented Gradients
• Tut 18: Xử lý ảnh - HOG - Huấn luyện mô hình phân loại người
• Tut 19: Xử lý ảnh - HOG - Phát hiện người
• Tut 20: Xử lý ảnh - Tổng hợp kinh nghiệm xử lý ảnh (End)
• Tut 21: Xử lý ảnh - Hiện thực trích đặc trưng Local Binary Patterns (LBP)
• Tut 22: Xử lý ảnh - Trích đặc trưng Gabor filters

Minh Nguyen

Share this:

      

• #xulyanh
• #opencv
• #imageprocessing