Trích đặc trưng Gabor filters (OpenCV)

Sep 5, 2020 2m 0

OpenCV - Tut 22: Gabor Filters

Tut 22: Gabor Filters

Hi các bẹn, lại là Minh huyền thoại đây. Bài viết này sẽ đi vào một phương pháp rút trích đặc trưng trong Xử Lý Ảnh, đó là phương pháp sử dụng các bộ lọc Gabor - còn gọi là Gabor filters.

Trích đặc trưng Gabor filter là gì?

Gabor filter là phương pháp trích đặc trưng dựa trên những bộ lọc, tên phương pháp này được đặt theo nhà vật lý học Dennis Gabor. Bộ lọc Gabor được cho là có khả năng phân tích hình ảnh tương tự hệ thống thị giác của con người. Thiết kế bộ lọc Gabor có công thức sau:

\[g(x, y) = e^{- \frac{a^2 + \gamma ^2b^2}{2 \sigma ^2} } e^{i (2 \pi \frac{a}{\lambda} + \psi )} (I)\]

với:

\[a = x \cos \theta + y \sin \theta\] \[b = -x \sin \theta + y \cos \theta\]

Công thức Gabor biểu diễn ở dạng số phức, mà số phức thì có phần thực và phần ảo.

Ta có:

\[e^{i \varphi } = \cos \varphi + i \sin \varphi (II)\]

Chứng minh và giải thích công thức (II): http://math2.org/math/oddsends/complexity/e%5Eitheta.htm

Theo (I) và (II) ta sẽ biểu diễn phần thực của bộ lọc Gabor theo công thức:

\[g(x, y) = e^{- \frac{a^2 + \gamma ^2b^2}{2 \sigma ^2} } \cos (2 \pi \frac{a}{\lambda} + \psi ) (III)\]

và phần ảo của bộ lọc Gabor theo công thức:

\[g(x, y) = e^{- \frac{a^2 + \gamma ^2b^2}{2 \sigma ^2} } \sin (2 \pi \frac{a}{\lambda} + \psi ) (IV)\]

Tham khảo: https://en.wikipedia.org/wiki/Gabor_filter

gaussian + cos=gabor filter

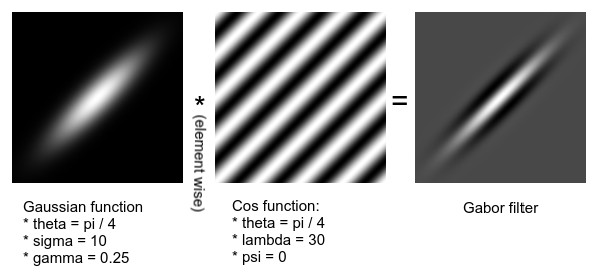
Ảnh. trực quan hóa bộ lọc Gabor filter cấu thành từ hàm Gaussian và hàm cos

Một số giải thích cho công thức bộ lọc Gabor:

a: chính là tích vô hướng của vector \((x, y)\) và vector \(\overrightarrow{Oa} = (\cos \theta, \sin \theta)\)
b: tương tự, đây là tích vô hướng của vector \((x, y)\) và vector \(\overrightarrow{Ob} = (-\sin \theta, \cos \theta)\). Để ý rằng, vector \(\overrightarrow{Oa}\) và vector \(\overrightarrow{Ob}\) vuông góc nhau (tích vô hướng của chúng bằng 1). Như vậy, ta có thể hiểu rằng (a, b) chính là điểm (x, y) đã được biến đổi từ gốc tọa độ Oxy sang gốc tọa độ mới là Oab, với \(\overrightarrow{Oa}\) và \(\overrightarrow{Ob}\) là các vector đơn vị. Khi \(\theta = 0\), thì \(x = a\) và \(y = b\). Oh wow! :).
\(\theta\) (theta): góc nghiêng của bộ lọc
Gabor được cấu thành từ tích của hàm Gaussian và hàm cos (phần thực), hàm sin (phần ảo). Tham khảo: Gaussian function
\(\sigma\) (sigma): độ lệch chuẩn trong công thức Gaussian
\(\gamma\) (gamma): quyết định hình dạng của Gaussian
Hàm sin / cos chính là công thức sóng: https://vi.wikipedia.org/wiki/S%C3%B3ng
\(\lambda\) (lambda): bước sóng
\(\psi\) (psi): pha ban đầu của sóng

Tinh chỉnh 5 tham số (\(\theta\), \(\sigma\), \(\gamma\), \(\lambda\), \(\psi\)) của bộ lọc Gabor sẽ cho ra hình dạng bộ lọc khác nhau. Tham khảo: https://medium.com/@anuj_shah/through-the-eyes-of-gabor-filter-17d1fdb3ac97

Sử dụng Gabor filter

Công thức Gabor với một bộ tham số sẽ tạo cho ta một bộ lọc đặc thù. Công dụng của Gabor filter là phát hiện cạnh (trích cạnh) của ảnh. Áp dụng bộ lọc Gabor vào ảnh ta sẽ sử dụng toán tử convolution.

Minh sẽ không hiện thực lại Gabor filter trong bài viết này vì đã có khá nhiều bản hiện thực sẵn trong các thư viện:

Code hiện thực Gabor filter trong Python (thư viện numpy): https://en.wikipedia.org/wiki/Gabor_filter
Gabor filter trong OpenCV (documentation): https://docs.opencv.org/4.4.0/d4/d86/group__imgproc__filter.html#gae84c92d248183bd92fa713ce51cc3599

Minh sẽ biểu diễn cách sử dụng bộ lọc Gabor để trích đặc trưng, sau đó lấy ảnh output trực quan hóa in ra để quan sát kết quả.

Ảnh mẫu full 100% bản quyền :">. Luận văn tốt nghiệp tui từng làm về bộ lọc Gabor này, nên quyết định "hy sinh vì nghệ thuật". Nay tạm bỏ nghề đi ăn cắp ảnh girl xinh (^___^)

minh.jpg

nguyen hoang minh

Chương trình bên dưới sẽ thực hiện các công việc sau:

Generate một dải (bank) bộ lọc Gabor theo 4 góc khác nhau 0, 45, 90 và 135 độ: generate_gabor_bank()
Áp dụng bộ lọc Gabor vào ảnh màu (3 kênh): apply_sliding_window_on_3_channels()
Trực quan hóa in ảnh kết quả. Lưu ý: bộ lọc Gabor Minh in ở góc trên bên trái của ảnh. Kích thước bộ lọc chỉ có 15x15 pixel nên nếu không để ý kĩ sẽ không nhìn thấy.
Trung bình các ảnh phân tích bởi bộ lọc Gabor được ảnh minh_avg.jpg

gabor.py

import time
import cv2
import numpy as np

IMAGE_PATH = "minh.jpg"

def scale_to_0_255(img):
    min_val = np.min(img)
    max_val = np.max(img)
    new_img = (img - min_val) / (max_val - min_val) # 0-1
    new_img *= 255
    return new_img

def apply_sliding_window_on_3_channels(img, kernel):
    # https://docs.opencv.org/4.4.0/d4/d86/group__imgproc__filter.html#ga27c049795ce870216ddfb366086b5a04
    layer_blue = cv2.filter2D(src=img[:,:,0], ddepth=-1, kernel=kernel)
    layer_green = cv2.filter2D(src=img[:,:,1], ddepth=-1, kernel=kernel)
    layer_red = cv2.filter2D(src=img[:,:,2], ddepth=-1, kernel=kernel)    
    
    new_img = np.zeros(list(layer_blue.shape) + [3])
    new_img[:,:,0], new_img[:,:,1], new_img[:,:,2] = layer_blue, layer_green, layer_red
    return new_img

def generate_gabor_bank(num_kernels, ksize=(15, 15), sigma=3, lambd=6, gamma=0.25, psi=0):
    bank = []
    theta = 0
    step = np.pi / num_kernels
    for idx in range(num_kernels):
        theta = idx * step
        # https://docs.opencv.org/4.4.0/d4/d86/group__imgproc__filter.html#gae84c92d248183bd92fa713ce51cc3599
        kernel = cv2.getGaborKernel(ksize=ksize, sigma=sigma, theta=theta, lambd=lambd, gamma=gamma, psi=psi)
        bank.append(kernel)
    return bank

def main():
    img = cv2.imread(IMAGE_PATH)
    gabor_bank = generate_gabor_bank(num_kernels=4)
    
    h, w, c = img.shape
    final_out = np.zeros([h, w*(len(gabor_bank)+1), c])
    final_out[:, :w, :] = img
    
    avg_out = np.zeros(img.shape)
    
    for idx, kernel in enumerate(gabor_bank):
        res = apply_sliding_window_on_3_channels(img, kernel)
        final_out[:, (idx+1)*w:(idx+2)*w, :] = res
        kh, kw = kernel.shape[:2]
        kernel_vis = scale_to_0_255(kernel)
        # https://numpy.org/doc/stable/reference/generated/numpy.expand_dims.html
        # https://numpy.org/doc/stable/reference/generated/numpy.repeat.html
        final_out[:kh, (idx+1)*w:(idx+1)*w+kw, :] = np.repeat(np.expand_dims(kernel_vis, axis=2), repeats=3, axis=2)        
        avg_out += res
        
    avg_out = avg_out / len(gabor_bank)
    avg_out = avg_out.astype(np.uint8)
    cv2.imwrite("minh_gabor.jpg", final_out)
    cv2.imwrite("minh_avg.jpg", avg_out)
    print("Saved @ minh_gabor.jpg")
    print("Saved @ minh_avg.jpg")
               
if __name__ == "__main__":
    start = time.time()
    main()
    end = time.time()
    elapsed_time = end - start
    print('Elapsed time: %.2f second' % elapsed_time)
    print('---------')
    print('* Follow me @ ' + "\x1b[1;%dm" % (34) + ' https://www.facebook.com/kyznano/' + "\x1b[0m")
    print('* Minh fanpage @ ' + "\x1b[1;%dm" % (34) + ' https://www.facebook.com/minhng.info/' + "\x1b[0m")    
    print('* Join GVGroup @ ' + "\x1b[1;%dm" % (34) + 'https://www.facebook.com/groups/ip.gvgroup/' + "\x1b[0m")    
    print('* Thank you ^^~')    

Thực thi code:

root@e7eba89aeeaf:/workspace/OPENCV/Gabor_filter# python gabor.py
Saved @ minh_gabor.jpg
Saved @ minh_avg.jpg
Elapsed time: 0.27 second
---------

Kết quả trực quan hóa:

result gabor filter on color image

Ảnh. Convolution dải bộ lọc Gabor (4 hướng)

result gabor filter combined

Ảnh. Trung bình các ảnh sau khi lọc với Gabor (4 hướng)

BONUS:

gabor filter on 16 orientations

Ảnh. Trích đặc trưng Gabor theo 16 hướng. Thấy rõ chữ trên áo của nam chính luôn :D.

Nhận xét:

Công thức Gabor khá tổng quát để tạo một bộ lọc trích cạnh.
Chủ động kiểm soát hướng của cạnh để trích xuất (đặc trưng) -> very powerful.
Kiểm soát được độ dày cạnh cần trích xuất.
Đặc trưng trích bởi Gabor filter có thể dùng để: đếm người (gián tiếp), OCR, nhận diện khuôn mặt, nhận diện cảm xúc, … -> có các bài báo trên mạng, bạn đọc tự tìm hiểu thêm.

Bài viết tiếp theo: Tut 23: Trích đặc trưng SIFT (coming soon)

Cảm ơn bạn đã theo dõi bài viết. Hãy kết nối với tớ nhé!

Minh: https://www.facebook.com/minhng.info
Khám phá xử lý ảnh - GVGroup: https://www.facebook.com/groups/ip.gvgroup

Khám phá xử lý ảnh - GVGroup

Danh sách bài viết series OpenCV:

Minh Nguyen

Trích đặc trưng Gabor filters (OpenCV)

Tut 22: Gabor Filters

Trích đặc trưng Gabor filter là gì?

Sử dụng Gabor filter

Share this:

Chuyển đổi ảnh OpenCV sang Pillow và ngược lại

Pha trộn ảnh trong OpenCV (blending)

Hiện thực trích đặc trưng Local Binary Patterns (LBP)

Quickly Set Up Odoo 18 in Docker: Install in Under 1 Minute

Docker for Odoo 17 - get Odoo within 1 minute

Giám sát Docker Container với Zabbix Agent 2

Kết nối pgAdmin vào PostgreSQL database của Odoo

Kết nối PostgreSQL database của Odoo bằng câu lệnh

Reduce swap usage