Đo góc của hai vector. Ứng dụng: Đo độ tương tự của 2 vector - cosine similarity
Công thức góc của 2 vector đơn giản mà ta đã học ở cấp 3, thực tế ứng dụng nó chính là công thức tính độ tương tự 2 vector: cosine similarity. Hãy xem ý nghĩa thực tiễn khi nào dùng đến nó.

Công thức tính góc của hai vector
\(similarity = \cos \theta = \frac{\overrightarrow{A} \cdot \overrightarrow{B}}{|\overrightarrow{A}||\overrightarrow{B}|}\).
Đây chỉ là 1 công thức toán lúc học cấp ba bình thường, nhưng thời điểm cấp ba đó ta chưa thấy nó có ứng dụng gì nhiều. Nó có liên quan đến tích vô hướng và ý nghĩa của nó.
Mãi cho đến khi Minh đắm chìm vào xử lý ảnh / thị giác máy tính thì mới thực sự hiểu tác dụng và biết khi nào nên dùng đến nó.
Ứng dụng đo độ tương tự hai vector
Bối cảnh bài toán nhận diện khuôn mặt
Giả sử ta đang làm 1 ứng dụng nhận diện khuôn mặt dùng AI (trí thông minh nhân tạo). Ứng dụng có tác dụng nhận diện mỗi tấm ảnh đưa vào là khuôn mặt của ai (danh tính). Ứng dụng dạng giống vầy :v
Video là tổng hợp của các hình ảnh liên tiếp, do đó bài toán của chúng ta được minh họa như ảnh sau:

Nếu đã làm qua xử lý ảnh, bạn sẽ biết rằng đầu ra của giải thuật nhận diện khuôn mặt chắc chắn sẽ phải có là 1 vector đặc trưng. Mỗi ảnh trong thư viện ảnh đã có và ảnh cần nhận diện sẽ chạy qua giải thuật trích đặc trưng (ngày nay người ta dùng deep learning) để có vector đặc trưng tương ứng.
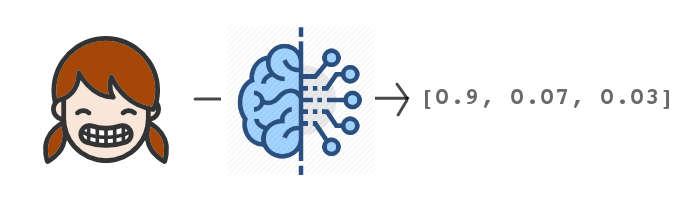
Như vậy ta có vector đặc trưng của mỗi khuôn mặt cần nhận diện. Xem hình minh họa bên dưới:

Phần tử thứ nhất trong vector mang ý nghĩa giá trị đại diện cho khuôn mặt của Ngân, giá trị này càng lớn thì đây càng có thể là Ngân. Tương tự, phần tử thứ hai trong vector đại diện cho Minh, phần tử thứ ba trong vector đại diện cho Nhung.
Với bối cảnh bài toán như trên ta chỉ còn bước cuối cùng là so trùng vector đặc trưng của mỗi hình ảnh cần dự đoán Đây là ai? với Danh tính đã có. OK, đây là lúc để tính độ tương tự giữa hai vector được trổ tài! Trong phạm vi bài viết này ta dùng cosine như công thức ở mục phía trên.
ps. Vì vector đặc trưng chưa thực sử ở dạng phân phối xác suất nên không thể đơn giản lấy phần tử lớn nhất được, đồng thời vector của các danh tính có thể là bất cứ chứ không phải chỉ đơn giản như bối cảnh bài toán nêu ra.
Tính cosine similarity
Bài toán trên đã được số hóa thành:
Ngân = [1, 0, 0]
Minh = [0, 1, 0]
Nhung = [0, 0, 1]
A = [0.9, 0.07, 0.03]
B = [0.02, 0.96, 0.04]
C = [0.1, 0.85, 0.05]
So trùng các vector A, B, C với các danh tính đã có Ngân, Minh, Nhung.
BÀI GIẢI
cos(A, Ngân) = 0.9964
cos(A, Minh) = 0.0775
cos(A, Nhung) = 0.0332
-> Kết luận: A là Ngân vì có độ tương đồng lớn nhất.
cos(B, Ngân) = 0.0208
cos(B, Minh) = 0.9989
cos(B, Nhung) = 0.0416
-> Kết luận: B là Minh vì có độ tương đồng lớn nhất.
cos(C, Ngân) = 0.1166
cos(C, Minh) = 0.9915
cos(C, Nhung) = 0.0583
-> Kết luận: C là Minh vì có độ tương đồng lớn nhất.
Vậy ta đã thấy ứng dụng cực kỳ thiết thực và quan trọng như thế nào của việc tính cosine góc giữa 2 vector.

Kết luận về độ đo góc giữa hai vector
- Giá trị cosine sẽ nằm trong [-1, 1]. Giá trị này càng lớn thể hiện độ tương đồng / giống nhau giữa 2 vector càng lớn.
- Ta dùng phép đo cosine similarity khi ta chỉ quan tâm về góc giữa 2 vector (KHÔNG QUAN TÂM về khoảng cách giữa 2 vector, nếu quan tâm về khoảng cách giữa 2 vector thì ta dùng phép tính khoảng cách Euclid). Nếu ta biểu diễn mỗi vector thành biểu đồ cột, thì ta đang muốn tính tương quan về hình dạng cột của 2 vector đó.
Các bài viết tham khảo thêm về Toán học:
- Đạo hàm là gì? Ý nghĩa của đạo hàm
- Vi phân là gì? Ứng dụng vi phân vào phép tính gần đúng
- Giới hạn của hàm số - lim
- Đạo hàm cấp cao và các công thức đạo hàm thường gặp
- Ý nghĩa của Tích Vô Hướng
- Trị riêng và vector riêng của ma trận
- Số phức là gì? Giải thích dễ hiểu về số phức
- Tổng hợp các dạng bài tập đạo hàm (2018)
- Đo góc của hai vector. Ứng dụng: Đo độ tương tự của 2 vector - cosine similarity
- Hoán vị, chỉnh hợp và tổ hợp
- Cách tính và ý nghĩa ma trận hiệp phương sai (covariance matrix)
- Tổng hợp các bài post toán học