Số phức là gì? Giải thích dễ hiểu về số phức
Số phức là gì? Số thực có thể được hình dung là những giá trị trong không gian 1 chiều, còn số phức chính là những giá trị nằm trong không gian 2 chiều gồm: trục thực và trục ảo.

Số phức
Định nghĩa số phức
Số phức có dạng \(a + bi\)
- a, b là các số thực
- i là đơn vị ảo
Với \(i^2 = -1\)
Nếu ta lấy phần thực của số phức thì đó là a. Nếu ta lấy phần ảo của số phức thì đó là b.
Ví dụ số phức:
- 2 + 3i –> phần thực: 2, phần ảo: 3
- 4 - 2i
- -5 + i
- -6 - 4i
- 1.2 + 5.1i
- 4.4 = 4.4 + 0i –> trong trường hợp này, hệ số b của đơn vị ảo bằng 0
Vậy ta có thể thấy rằng số phức là trường hợp tổng quát hơn của số thực. Số thực là 1 trường hợp cụ thể của số phức (khi b = 0). Để dễ hình dung nhất về số phức. Ta tiến hành so sánh và minh họa cụ thể chúng trong không gian 2 chiều trong phần tiếp theo.
Điểm khác giữa số phức và số thực
Tự nhiên thêm đơn vị ảo i vào làm chi không biết (=__=), làm ta rất khó hình dung nếu chỉ nhìn cách biểu diễn con số phức và các công thức tính toán của nó. Nào ta hãy cùng biểu diễn / visualize con số phức đó lên không gian 2 chiều (mặt phẳng) cho dễ tưởng tượng nhé!
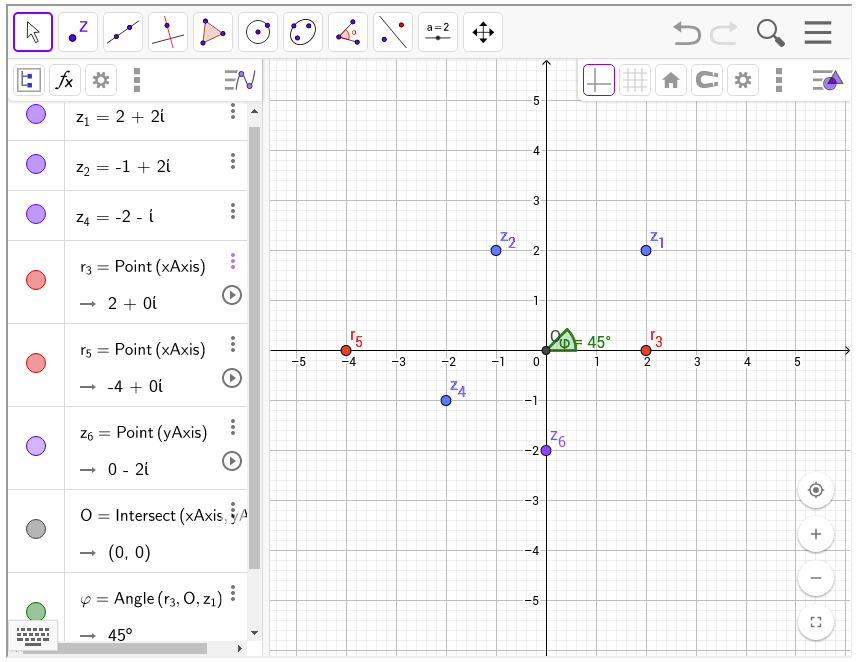
Như hình minh họa trên, trục x (trục hoành) biểu diễn cho phần thực, còn trục y (trục tung) biểu diễn cho phần ảo. Những con số thực mà ta tính toán trước kia sẽ giống như \(r_3\), \(r_5\) được biểu diễn như trên hình trong không gian phức.
\[(z_6)^2 = (0 - 2i)^2 = (-2i)^2 = 4i^2 = 4(-1) = -4 = r_5\]Dạng lượng giác của số phức
\(z = r(cos \varphi + isin \varphi) = rcos \varphi + r*i*sin \varphi\)
với r là 1 số thực, \(\varphi\) là góc.
So sánh với định nghĩa, ta thấy rằng:
- Phần thực: \(a = rcos \varphi\)
- Phần ảo: \(b = rsin \varphi\)
Điểm đặc biệt là số phức ở dạng lượng giác được biểu diễn theo độ dài vector (r) và góc của vector (\(\varphi\)).
Xem Z là điểm có tọa độ \((rcos \varphi, rsin \varphi)\).Thật vậy: \(| \overrightarrow{OZ} | = \sqrt{(rcos \varphi)^2 + (rsin \varphi)^2} = \sqrt{(r^2((cos \varphi)^2 + (sin \varphi)^2)} = \sqrt{(r^2(1)} = r\)
Góc tạo bởi OZ và Ox là:
\[\arctan (\frac{Z_y}{Z_x}) = \arctan (\frac{rsin \varphi}{rcos \varphi}) = \arctan (tan \varphi) = \varphi\]Với ví dụ hình minh họa ở mục trên, số phức \(z_1 = 2 + 2i\) sẽ được biểu diễn ở dạng lượng giác là: \(r = \sqrt{2^2 + 2^2} = 2\sqrt{2}\)
\[\varphi = \arctan (\frac{2}{2}) = \frac{\pi}{4}\] \[z_1 = 2\sqrt{2}(cos \frac{\pi}{4} + isin \frac{\pi}{4})\]Nếu thấy hay và dễ hiểu, hãy share cho các bạn cùng lớp nhé! (^^)
Các bài viết tham khảo thêm về Toán học:
- Đạo hàm là gì? Ý nghĩa của đạo hàm
- Vi phân là gì? Ứng dụng vi phân vào phép tính gần đúng
- Giới hạn của hàm số - lim
- Đạo hàm cấp cao và các công thức đạo hàm thường gặp
- Ý nghĩa của Tích Vô Hướng
- Trị riêng và vector riêng của ma trận
- Số phức là gì? Giải thích dễ hiểu về số phức
- Tổng hợp các dạng bài tập đạo hàm (2018)
- Đo góc của hai vector. Ứng dụng: Đo độ tương tự của 2 vector - cosine similarity
- Hoán vị, chỉnh hợp và tổ hợp
- Cách tính và ý nghĩa ma trận hiệp phương sai (covariance matrix)
- Tổng hợp các bài post toán học