Ý nghĩa của Tích Vô Hướng
Cách tính toán tích vô hướng của 2 vector và phân tích ý nghĩa của nó.

Tích vô hướng
Định nghĩa đại số:
\(\overrightarrow{a} \cdot \overrightarrow{b} = \sum_{i=1}^{n} a_ib_i = a_1b_1 + a_2b_2 + ... + a_nb_n\).
Ví dụ:
\(\overrightarrow{a} = [1, -2, -3, 5]\).
\(\overrightarrow{b} = [3, 4, -1, -2]\).
\(\overrightarrow{a} \cdot \overrightarrow{b} = 1*3 + (-2)*4 + (-3)*(-1) + 5*(-2) = -12\).
Định nghĩa hình học:
\(\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}||\overrightarrow{b}|\cos \theta\).
với:
- |\(\overrightarrow{a}\)|: độ lớn vector a
- |\(\overrightarrow{b}\)|: độ lớn vector b
- \(\theta\): góc tạo bởi 2 vector a và b
(Tham khảo: [Tích vô hướng - Wikipedia][Tích vô hướng - Wikipedia])
Ý nghĩa tích vô hướng
Tích vô hướng là tích của: độ lớn của vector và độ lớn của phép chiếu vô hướng (vuông góc) của vector còn lại lên nó.
Cho các vector 2 chiều: \(\overrightarrow{A}\) và \(\overrightarrow{B}\). Theo định nghĩa hình học ta có:
\(\overrightarrow{A} \cdot \overrightarrow{B} = |\overrightarrow{A}||\overrightarrow{B}|\cos \theta\).
Nếu ta chiếu \(\overrightarrow{A}\) vuông góc lên \(\overrightarrow{B}\), ta sẽ thấy rằng |\(\overrightarrow{A}\)|\(\cos \theta\) chính là độ lớn của hình chiếu của \(\overrightarrow{A}\) trên \(\overrightarrow{B}\).
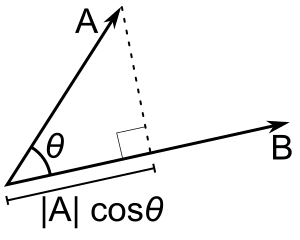
Ngược lại, nếu ta chiếu \(\overrightarrow{B}\) vuông góc lên \(\overrightarrow{A}\), ta sẽ thấy rằng |\(\overrightarrow{B}\)|\(\cos \theta\) chính là độ lớn của hình chiếu của \(\overrightarrow{B}\) trên \(\overrightarrow{A}\).
Như vậy, ta có thể hiểu nôm na tích vô hướng của 2 vector là:
Chiếu 1 vector này lên vector còn lại, sau đó lấy độ lớn của vector hình chiếu nhân cho độ lớn của vector còn lại.
Kết quả của tích vô hướng (tiếng Anh: dot product / scalar product) là 1 con số (scalar). Con số này thể hiện sự tương quan về hướng và độ lớn của 2 vector đó.
(Để dễ nhớ phân biệt với tích có hướng, tích vô hướng –> có từ vô hướng –> nghĩa là không có hướng –> kết quả là 1 con số)
Ví dụ:
\[\overrightarrow{A} = [5, 0], \overrightarrow{B} = [-2, 2], \overrightarrow{A} \cdot \overrightarrow{B} = -10\]Ý nghĩa của con số -10 phía trên:
- Là 1 số âm –> vector A và B ngược hướng nhau.
- |-10| = 10 (giá trị tuyệt đối) –> càng lớn thể hiện mức độ về độ lớn của vector thành phần (|\(\overrightarrow{A}\)| = 5, |hình chiếu vector B trên A| = 2). Ta không thể phán xét gì thêm bởi vì 10 có thể bằng 5 * 2 hoặc bằng 1 * 10 hoặc bằng tích của 2 con số nào đó.
Như vậy, tích vô hướng (gọi là D = \(\overrightarrow{A} \cdot \overrightarrow{B}\)) thể hiện ý nghĩa:
- Tương quan về hướng
- Giá trị dương (D > 0): 2 vector cùng hướng.
- Giá trị âm (D < 0): 2 vector ngược hướng.
- Giá trị bằng 0 (D = 0): 2 vector vuông góc.
- Tương quan về độ lớn của 2 vector
- Giá trị càng lớn (|D| lớn): độ lớn của 1 trong 2 vector rất lớn hoặc độ lớn của hình chiếu vector này lên vector kia rất lớn.
- Giá trị càng nhỏ (|D| nhỏ): độ lớn của 1 trong 2 vector rất nhỏ hoặc độ lớn của hình chiếu vector này lên vector kia rất nhỏ.
Nói cách khác, 2 vector càng giống / tương tự nhau thì tích vô hướng của chúng càng lớn.
Các bài viết tham khảo thêm về Toán học:
- Đạo hàm là gì? Ý nghĩa của đạo hàm
- Vi phân là gì? Ứng dụng vi phân vào phép tính gần đúng
- Giới hạn của hàm số - lim
- Đạo hàm cấp cao và các công thức đạo hàm thường gặp
- Ý nghĩa của Tích Vô Hướng
- Trị riêng và vector riêng của ma trận
- Số phức là gì? Giải thích dễ hiểu về số phức
- Tổng hợp các dạng bài tập đạo hàm (2018)
- Đo góc của hai vector. Ứng dụng: Đo độ tương tự của 2 vector - cosine similarity
- Hoán vị, chỉnh hợp và tổ hợp
- Cách tính và ý nghĩa ma trận hiệp phương sai (covariance matrix)
- Tổng hợp các bài post toán học